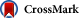Selection maintaining protein stability at equilibrium
Highlights
- •
Protein stability is kept at equilibrium by random drift and positive selection.
- •
Neutral selection is predominant only for low-abundant, non-essential proteins.
- •
Protein abundance more decreases evolutionary rate for less-constrained proteins.
- •
Structural constraint more decreases evolutionary rate for less-abundant, less-essential proteins.
- •
Protein stability (−ΔGe/kT) and 〈Ka/Ks〉 are predicted to decrease as growth temperature increases.
Abstract
The common understanding of protein evolution has been that neutral mutations are fixed by random drift, and a proportion of neutral mutations depending on the strength of structural and functional constraints primarily determines evolutionary rate. Recently it was indicated that fitness costs due to misfolded proteins are a determinant of evolutionary rate and selection originating in protein stability is a driving force of protein evolution. Here we examine protein evolution under the selection maintaining protein stability.
Protein fitness is a generic form of fitness costs due to misfolded proteins; ![]() , where s and ΔΔG are selective advantage and stability change of a mutant protein, ΔG is the folding free energy of the wildtype protein, and κ is a parameter representing protein abundance and indispensability. The distribution of ΔΔG
is approximated to be a bi-Gaussian distribution, which represents
structurally slightly- or highly-constrained sites. Also, the mean of
the distribution is negatively proportional to ΔG.
, where s and ΔΔG are selective advantage and stability change of a mutant protein, ΔG is the folding free energy of the wildtype protein, and κ is a parameter representing protein abundance and indispensability. The distribution of ΔΔG
is approximated to be a bi-Gaussian distribution, which represents
structurally slightly- or highly-constrained sites. Also, the mean of
the distribution is negatively proportional to ΔG.
The evolution of this gene has an equilibrium point (ΔGe) of protein stability, the range of which is consistent with observed values in the ProTherm database. The probability distribution of Ka/Ks, the ratio of nonsynonymous to synonymous substitution rate per site, over fixed mutants in the vicinity of the equilibrium shows that nearly neutral selection is predominant only in low-abundant, non-essential proteins of ΔGe>−2.5 kcal/mol. In the other proteins, positive selection on stabilizing mutations is significant to maintain protein stability at equilibrium as well as random drift on slightly negative mutations, although the average 〈Ka/Ks〉 is less than 1. Slow evolutionary rates can be caused by both high protein abundance/indispensability and large effective population size, which produces positive shifts of ΔΔG through decreasing ΔGe, and strong structural constraints, which directly make ΔΔG more positive. Protein abundance/indispensability more affect evolutionary rate for less constrained proteins, and structural constraint for less abundant, less essential proteins. The effect of protein indispensability on evolutionary rate may be hidden by the variation of protein abundance and detected only in low-abundant proteins. Also, protein stability (−ΔGe/kT) and 〈Ka/Ks〉 are predicted to decrease as growth temperature increases.
Keywords
- Neutral theory;
- Positive selection;
- Evolutionary rate;
- Structural constraints;
- Protein abundance
1. Introduction
The common understanding of protein evolution has been that amino acid substitutions observed in homologous proteins are selectively neutral (Kimura, 1968, Kimura, 1969, Kimura and Ohta, 1971 and Kimura and Ohta, 1974) or slightly deleterious (Ohta, 1973 and Ohta, 1992), and random drift is a primary force to fix amino acid substitutions in population. The rate of protein evolution has been understood to be determined primarily by the proportion of neutral mutations, which may be measured by the ratio of nonsynonymous to synonymous substitution rate per site (Ka/Ks) (Miyata and Yasunaga, 1980) and determined by functional density (Zuckerkandl, 1976) weighted by the relative variability at specific-function sites of a protein (Go and Miyazawa, 1980). Since then, these theories have been widely accepted, however, recently a question has been raised on whether the diversity of protein evolutionary rate among genes can be explained only by the proportion and the variability of specific-function sites, and molecular and population-genetic constraints on protein evolutionary rate have been explored.
Recent works have revealed that protein evolutionary rate is correlated with gene expression level; highly expressed genes evolve slowly, accounting for as much as 34% of rate variation in yeast (Pál et al., 2001). Of course, there are many reports that support a principle of lower evolution rate for stronger functional density. Broadly expressed proteins in many tissues tend to evolve slower than tissue-specific ones (Kuma et al., 1995 and Duret and Mouchiro, 2000). The connectivity of well-conserved proteins in a network is shown (Fraser et al., 2002) to be negatively correlated with their rate of evolution, because a greater proportion of the protein sequence is directly involved in its function. A fitness cost due to protein–protein misinteraction affects the evolutionary rate of surface residues (Yang et al., 2012). Protein dispensability in yeast is correlated with the rate of evolution (Hirsh and Fraser, 2001 and Hirsh and Fraser, 2003), although there is a report insisting on no correlation between them (Pál et al., 2003). Other reports indicate that the correlation between gene dispensability and evolutionary rate, although low, is significant (Zhang and He, 2005, Wall et al., 2005 and Jordan et al., 2002).
It was proposed (Drummond et al., 2005, Drummond and Wilke, 2008 and Geiler-Samerotte et al., 2011) that low substitution rates of highly expressed genes could be explained by fitness costs due to functional loss and toxicity (Stoebel et al., 2008 and Geiler-Samerotte et al., 2011) of misfolded proteins. Misfolding reduces the concentration of functional proteins, and wastes cellular time and energy on production of useless proteins. Also misfolded proteins form insoluble aggregates (Geiler-Samerotte et al., 2011). Fitness cost due to misfolded proteins is larger for highly expressed genes than for less expressed ones.
Fitness cost due to misfolded proteins was formulated (Drummond and Wilke, 2008 and Geiler-Samerotte et al., 2011) to be related to the proportion of misfolded proteins. Knowledge of protein folding indicates that protein folding primarily occurs in two-state transition (Miyazawa and Jernigan, 1982a and Miyazawa and Jernigan, 1982b), which means that the ensemble of protein conformations are a mixture of completely folded and unfolded conformations. Free energy (ΔG) of protein stability, which is equal to the free energy of the denatured state subtracted from that of the native state, and stability change (ΔΔG) due to amino acid substitutions are collected in the ProTherm database (Kumar et al., 2006), although the data are not sufficient. Prediction methods, however, for ΔΔG are improved enough to reproduce real distributions of ΔΔG (Schymkowitz et al., 2005 and Yin et al., 2007). Therefore, on the biophysical basis, the distribution of fitness can be estimated and protein evolution can be studied. Shakhnovich group studied protein evolution on the basis of knowledge of protein folding (Serohijos and Shakhnovich, 2014 and Dasmeh et al., 2014) and showed (Serohijos et al., 2012) that the negative correlation between protein abundance and Ka/Ks was caused by the distribution of ΔΔG that negatively correlates with the ΔG of a wild type. Also, it was shown (Serohijos et al., 2013) that highly abundant proteins had to be more stable than low abundant ones. Relationship between evolutionary rate and protein stability is studied from various points of view (Echave et al., 2015 and Faure and Koonin, 2015).
Here
we study relationship between evolutionary rate and selection on
protein stability in a monoclonal approximation. A fitness assumed here
for a protein is a generic form to which all formulations (Drummond and Wilke, 2008, Geiler-Samerotte et al., 2011, Serohijos et al., 2012, Serohijos et al., 2013, Serohijos and Shakhnovich, 2014 and Dasmeh et al., 2014) previously employed for protein fitness are reduced in the condition of exp(βΔG)⪡1, which is satisfied in the typical range of folding free energies shown in Fig. 1; β=1/(kT), k is the Boltzmann constant and T is absolute temperature. The generic form of Malthusian fitness of a protein-coding gene is ![]() , where κ
is a parameter, which may be a function of protein abundance and
dispensability; see Methods for details. The distribution of stability
change ΔΔG due to single amino acid substitutions is approximated as a weighted sum of two Gaussian functions that was shown (Tokuriki et al., 2007) to well reproduce actual distributions of ΔΔG.
One of the two Gaussian functions describes substitutions at
structurally less-constrained surface sites, and the other at
more-constrained core sites of proteins. The proportion of
less-constrained surface sites is a parameter (θ).
, where κ
is a parameter, which may be a function of protein abundance and
dispensability; see Methods for details. The distribution of stability
change ΔΔG due to single amino acid substitutions is approximated as a weighted sum of two Gaussian functions that was shown (Tokuriki et al., 2007) to well reproduce actual distributions of ΔΔG.
One of the two Gaussian functions describes substitutions at
structurally less-constrained surface sites, and the other at
more-constrained core sites of proteins. The proportion of
less-constrained surface sites is a parameter (θ).

- Fig. 1.
Distribution of folding free energies of monomeric protein families. Stability data of monomeric proteins for which the item of dG_H2O or dG was obtained in the experimental condition of 6.7≤pH≤7.3 and
 and their folding-unfolding transition is two state and reversible are extracted from the ProTherm (Kumar et al., 2006);
in the case of dG only thermal transition data are used. Thermophilic
proteins, and proteins observed with salts or additives are also
removed. An equal sampling weight is assigned to each species of
homologous protein, and the total sampling weight of each protein family
is normalized to one. In the case in which multiple data exist for the
same species of protein, its sampling weight is divided to each of the
data. However, proteins whose stabilities are known may be samples
biased from the protein universe. The value, ΔGe=−5.24, kcal/mol of equilibrium stability at the representative parameter values,
and their folding-unfolding transition is two state and reversible are extracted from the ProTherm (Kumar et al., 2006);
in the case of dG only thermal transition data are used. Thermophilic
proteins, and proteins observed with salts or additives are also
removed. An equal sampling weight is assigned to each species of
homologous protein, and the total sampling weight of each protein family
is normalized to one. In the case in which multiple data exist for the
same species of protein, its sampling weight is divided to each of the
data. However, proteins whose stabilities are known may be samples
biased from the protein universe. The value, ΔGe=−5.24, kcal/mol of equilibrium stability at the representative parameter values,  and θ=0.53, agrees with the most probable value of ΔG in the distribution above. Also, the range of ΔG shown above is consistent with that range, −2 to
and θ=0.53, agrees with the most probable value of ΔG in the distribution above. Also, the range of ΔG shown above is consistent with that range, −2 to  , expected from the present model. The kcal/mol unit is used for ΔG. A similar distribution was also compiled (Zeldovich et al., 2007).
, expected from the present model. The kcal/mol unit is used for ΔG. A similar distribution was also compiled (Zeldovich et al., 2007).
The fixation probability of a mutant with ΔΔG can be calculated for a duploid population with effective population size Ne (Crow and Kimura, 1970). In the population of genes with such a fitness protein stability is evolutionarily maintained at equilibrium, and equilibrium stability (ΔGe) negatively correlates with protein abundance/dispensability (κ ). The range of ΔGe is consistent with the observed range of folding free energies shown in Fig. 1.
The probability density functions (PDF) of Ka/Ks, the ratio of nonsynonymous to synonymous substitution rate per site (Miyata and Yasunaga, 1980), at equilibrium and also in the vicinity of equilibrium are numerically examined over a whole domain of the parameters, ![]() and 0≤θ≤1.
The dependences of evolutionary rate on protein
abundance/dispensability and on structural constraint are quantitatively
described, and it is shown that both factors cannot be ignored on
protein evolutionary rate, although protein abundance/indispensability
more affect evolutionary rate for less constrained proteins, and
structural constraint for less abundant, less essential proteins. Like
protein abundance, protein indispensability must correlate with
evolutionary rate, but a correlation between them may be hidden by the
variation of protein abundance as well as effective population size, and
detected only in low-abundant proteins. It has also become clear that
nearly neutral selection is predominant only in low-abundant,
non-essential proteins with
and 0≤θ≤1.
The dependences of evolutionary rate on protein
abundance/dispensability and on structural constraint are quantitatively
described, and it is shown that both factors cannot be ignored on
protein evolutionary rate, although protein abundance/indispensability
more affect evolutionary rate for less constrained proteins, and
structural constraint for less abundant, less essential proteins. Like
protein abundance, protein indispensability must correlate with
evolutionary rate, but a correlation between them may be hidden by the
variation of protein abundance as well as effective population size, and
detected only in low-abundant proteins. It has also become clear that
nearly neutral selection is predominant only in low-abundant,
non-essential proteins with ![]() or ΔGe>−2.5 kcal/mol,
and in the other proteins positive selection is significant to more
stabilize a less-stable wild type. Also, a significant amount of
slightly negative mutants are fixed in population by random drift. This
view of protein evolution is contrary to the previous understanding. The
present model based on a biophysical knowledge of protein stability
also indicates that protein stability (−βΔGe) and the average of Ka/Ks decrease as growth temperature increases.
or ΔGe>−2.5 kcal/mol,
and in the other proteins positive selection is significant to more
stabilize a less-stable wild type. Also, a significant amount of
slightly negative mutants are fixed in population by random drift. This
view of protein evolution is contrary to the previous understanding. The
present model based on a biophysical knowledge of protein stability
also indicates that protein stability (−βΔGe) and the average of Ka/Ks decrease as growth temperature increases.
2. Methods
2.1. Fitness costs due to misfolded proteins
Misfolding can impose costs in three distinct ways (Geiler-Samerotte et al., 2011); loss of function, diversion of protein synthesis resources away from essential proteins, and toxicity of the misfolded molecules. Fitness cost due to functional loss was formulated (Drummond and Wilke, 2008) by taking account of protein dispensability. Assuming that fitness cost of each gene is additive in the Malthusian fitness scale, the total Malthusian fitness of a genome was estimated as
Protein folding primarily occurs in the two-state transition, which means that protein conformations are a mixture of completely folded and unfolded conformations (Miyazawa and Jernigan, 1982a and Miyazawa and Jernigan, 1982b). Therefore, if the completely folded (native) state is more stable by a free energy difference ΔG than the unfolded (denatured) state, then the native fraction in the conformational ensemble will be equal to
where β=1/kT; k is the Boltzmann constant and T is absolute temperature.Thus, Eq. (1) for the Malthusian fitness of a genome can be transformed as follows in terms of the folding free energy ΔG of the native conformation:
Because ofDrummond and Wilke (2008) took notice of toxicity of misfolded proteins as well as diversion of protein synthesis resources, and formulated the Malthusian fitness (mmisfolds) of a genome to be negatively proportional to the total amount of misfolded proteins, which must be produced to obtain the necessary amount of folded proteins (Serohijos et al., 2012):
where c is a positive constant and assumed to be c=0.0001, and Ai is the abundance of protein i.2.2. Fitness of a linear metabolic pathway
Serohijos and Shakhnovich (2014) examined the evolution of a linear metabolic pathway whose Wrightian fitness was defined as
where εi was defined as enzyme efficiency and assumed to be εi=1. The wflux is a fitness originating from the enzymatic flux of a linear metabolic pathway, and wmisfolds represents the effect of toxicity of misfolded proteins, and is the same functional form as Eq. (1), although Eq. (1) is a definition for Malthusian fitness. Then, the Malthusian fitness corresponding to the Wrightian fitness above can be represented as
2.3. Other formulations of protein fitness
Also, the following simple definition for fitness to maintain protein stability was used (Dasmeh et al., 2014):


In addition, Eq. (3) for functional loss was employed with γi⇒cAi to represent toxicity of misfolded proteins in (Serohijos et al., 2012 and Serohijos et al., 2013).
2.4. A generic form of protein fitness
Thus, all expressions above for Malthusian fitness of protein can be well approximated by the following expression, because of exp(βΔG)⪡1 in the typical range of folding free energies shown in Fig. 1:
where κi is a parameter. If the fitness costs of functional loss and toxicity due to misfolded proteins are taken into account, κi will be defined as
The selective advantage of a mutant, in which each protein is destabilized by ΔΔGi, to the wild type can be represented by
3. Results
3.1. Protein stability and fitness
Here, we consider the evolution of a single protein-coding gene in which the selective advantage of mutant proteins in Malthusian parameters is assumed to be
and therefore s is upper-bounded by

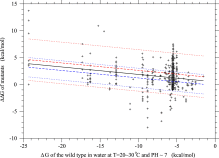
Based on measurements of stability changes due to single amino acid substitutions in proteins, which are collected in the ProTherm database (Kumar et al., 2006), Serohijos et al. (2012) reported that the distribution of ΔΔG is approximately a Gaussian distribution with mean=1 kcal/mol and standard deviation=1.7 kcal/mol. In addition, it was shown (Serohijos et al., 2012) that the mean of ΔΔG is negatively proportional to ΔG, and that this dependence of the mean of ΔΔG on ΔG is not large but still important to cause the observed negative correlation between protein abundance and evolutionary rate. On the other hand, (Tokuriki et al., 2007) computationally predicted ΔΔG for all possible single amino acid substitutions in 21 different globular, single domain proteins, and showed that the predicted distributions of ΔΔG were strikingly similar despite a range of protein sizes and folds and largely follow a bi-Gaussian distribution: one of the two Gaussian distributions results from substitutions on protein surfaces and is a narrow distribution with a mildly destabilizing mean ΔΔG, whereas the other due to substitutions in protein cores is a wider distribution with a stronger destabilizing mean (Tokuriki et al., 2007).
Here, according to Tokuriki et al. (2007), the distribution of ΔΔG due to single amino acid substitutions is approximated as a bi-Gaussian function with the dependence of mean ΔΔG on ΔG, in order to examine the effects of structural constraint on evolutionary rate. The probability density function (PDF) of ΔΔG, p(ΔΔG), for nonsynonymous substitutions is assumed to be

- 1.
Equations (23) and (24) satisfy μs(ΔG0)=0.56 and μc(ΔG0)=1.96, which were estimated for single nucleotide substitutions in Tokuriki et al. (2007), at a certain value (ΔG0) of ΔG.
- 2.
The total mean of the two Gaussian functions agrees with the regression line, μ=−0.14ΔG+0.49. The value of θ is taken to be 0.53, which is equal to the average of θ over proteins used in Tokuriki et al. (2007).

- Fig. 2.
Dependence of stability changes, ΔΔG, due to single amino acid substitutions on the protein stability, ΔG, of the wild type. A solid line shows the regression line, ΔΔG=−0.14ΔG+0.49; the correlation coefficient and p -value are equal to −0.20 and <10−7, respectively. Broken lines show two means of bi-Gaussian distributions, μs in blue and μc in red. Blue dotted lines show μs±2σs and red dotted lines μc±2σc. See Eqs. (22), (23) and (24) for the bi-Gaussian distribution. Stability data of single amino acid mutants for which the items dG_H2O and ddG_H2O or dG and ddG were obtained in the experimental condition of 6.7≤pH≤7.3 and
 and their folding-unfolding transitions are two state and reversible are extracted from the ProTherm (Kumar et al., 2006).
In the case of dG only thermal transition data are used. In the case in
which multiple data exist for the same protein, only one of them is
used. The kcal/mol unit is used for ΔΔG and ΔG. A similar distribution was also compiled (Serohijos et al., 2012).
(For interpretation of the references to color in this figure caption,
the reader is referred to the web version of this paper.)
and their folding-unfolding transitions are two state and reversible are extracted from the ProTherm (Kumar et al., 2006).
In the case of dG only thermal transition data are used. In the case in
which multiple data exist for the same protein, only one of them is
used. The kcal/mol unit is used for ΔΔG and ΔG. A similar distribution was also compiled (Serohijos et al., 2012).
(For interpretation of the references to color in this figure caption,
the reader is referred to the web version of this paper.)
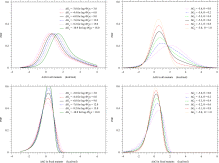
The dependence of the PDF, p(ΔΔG), of ΔΔG on θ is shown in Fig. 3. Also, the PDF of selective advantage, p(4Nes)=−p(ΔΔG)dΔΔG/d4Nes, is shown in Fig. S.4 to have a peak at a small, positive value of selective advantage, which moves toward more positive values as θ and/or 4Neκ increase.

- Fig. 3.
PDFs of stability changes, ΔΔG, due to single amino acid substitutions in all mutants and in fixed mutants at equilibrium of protein stability, ΔG=ΔGe. The PDF of ΔΔG due to single amino acid substitutions in all arising mutants is assumed to be bi-Gaussian; see Eq. (22). Unless specified,
 and θ=0.53 are employed. The kcal/mol unit is used for ΔΔG and ΔGe.
and θ=0.53 are employed. The kcal/mol unit is used for ΔΔG and ΔGe.
3.2. Equilibrium state of protein stability in protein evolution
The fixation probability u for a mutant gene with selective advantage s and gene frequency q in a duploid system of effective population size Ne was given as a function of 4Nes and q by ( Crow and Kimura, 1970)
where q=1/(2N) for a single mutant gene in a population of size N . Population size is taken to be N=106. The ratio of the substitution rate per nonsynonymous site (Ka) for nonsynonymous substitutions with selective advantage s to the substitution rate per synonymous site (Ks) for nonsynonymous substitutions with s=0 isassuming that synonymous substitutions are completely neutral and mutation rates at both types of sites are the same. Equations (19) and (25) indicate that 4Neκ can be regarded as a single parameter for Ka/Ks. Furthermore, if the dependence of the mean ΔΔG on ΔG could be neglected, 4Neκexp(βΔG) could be regarded as a single parameter. In the range of |4Nesq|/2⪡1, both Ka/Ks and the PDF of Ka/Ks do not depend on q=1/(2N); see Eq. (27) and (S.15).The PDF of ΔΔG of fixed mutant genes, p(ΔΔGfixed), is
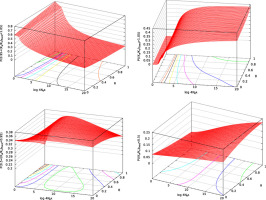
where 〈u〉 is the average fixation rate. Fig. 3 shows the PDF of ΔΔG of fixed mutant genes. The PDF of 4Nes in fixed mutants is also shown in Fig. S.4; p(4Nesfixed)=−p(ΔΔGfixed)dΔΔG/d4Nes. Then, the average of ΔΔG in fixed mutant genes can be calculated;Fig. 4 shows the average of the ΔΔG over fixed mutant genes, 〈ΔΔG〉fixed, to monotonically decrease with ΔG, indicating that the temporal process of ΔG is stable at 〈ΔΔG〉fixed(ΔGe)=0 due to the balance between random drift on destabilizing mutations and positive selection on stabilizing mutations; ΔGe is the folding free energy at the equilibrium state. If a wild-type protein becomes less stable than the equilibrium, ΔG>ΔGe, more stabilizing mutants will fix due to primarily positive selection and secondarily random drift, because stabilizing mutants will increase due to negative shifts of ΔΔG and also the effect of stability change on selective advantage will be more amplified; see Eqs. (23) and (24) for the dependence of ΔΔG on ΔG, and Eq. (19) for the fitness of stability change. As shown in Fig. S.6, the probability of Ka/Ks>1.0, that is, positive selection, significantly increases as ΔG becomes more positive than the equilibrium stability ΔGe. On the other hand, if a wild-type protein becomes more stable than the equilibrium, ΔG<ΔGe, more destabilizing mutants will fix due to random drift, because destabilizing mutants will increase due to positive shifts of ΔΔG and also more destabilizing mutants become nearly neutral due to the less-amplified effect of stability change on selective advantage. As shown later, the PDF of Ka/Ks in the vicinity of equilibrium confirms this mechanism for maintaining protein stability at equilibrium.
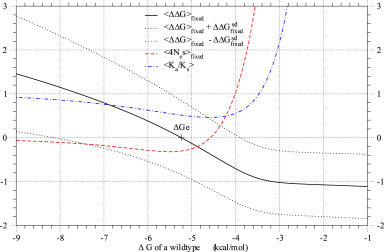
- Fig. 4.
The average, 〈ΔΔG〉fixed, of stability changes over fixed mutants versus protein stability, ΔG, of the wild type. ΔGe, where 〈ΔΔG〉=0, is the stable equilibrium value of folding free energy, ΔG, in protein evolution. The averages of ΔΔG, 4Nes, and Ka/Ks over fixed mutants are plotted against protein stability, ΔG, of the wild type by solid, broken, and dash-dot lines, respectively. Thick dotted lines show the values of
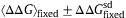 , where
, where 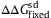 is the standard deviation of ΔΔG over fixed mutants.
is the standard deviation of ΔΔG over fixed mutants. 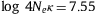 and θ=0.53 are employed. The kcal/mol unit is used for ΔΔG and ΔG.
and θ=0.53 are employed. The kcal/mol unit is used for ΔΔG and ΔG.
It was claimed (Serohijos et al., 2012 and Serohijos et al., 2013) that the equilibrium point would correspond to the minimum of the average fixation probability. However, in Fig. 4 for ![]() and θ=0.53, the average 〈s〉fixed of selective advantage in fixed mutants has a minimum at ΔG=−5.50 kcal/mol and changes its sign at ΔG=−4.58 kcal/mol, where the average 〈Ka/Ks〉=〈u〉/q has a minimum and which is more positive than the equilibrium stability ΔGe=−5.24 kcal/mol. In other words, Fig. 4 and Fig. S.16 show that the values of ΔG at 〈ΔΔG〉fixed=0 and at the minimum of 〈Ka/Ks〉 may be close but differ from each other, and indicate that the value of ΔG corresponding to the minimum of 〈Ka/Ks〉 is not a good approximation for the equilibrium stability, because 〈Ka/Ks〉 gently changes in the vicinity of the equilibrium stability as shown in Fig. S.16.
and θ=0.53, the average 〈s〉fixed of selective advantage in fixed mutants has a minimum at ΔG=−5.50 kcal/mol and changes its sign at ΔG=−4.58 kcal/mol, where the average 〈Ka/Ks〉=〈u〉/q has a minimum and which is more positive than the equilibrium stability ΔGe=−5.24 kcal/mol. In other words, Fig. 4 and Fig. S.16 show that the values of ΔG at 〈ΔΔG〉fixed=0 and at the minimum of 〈Ka/Ks〉 may be close but differ from each other, and indicate that the value of ΔG corresponding to the minimum of 〈Ka/Ks〉 is not a good approximation for the equilibrium stability, because 〈Ka/Ks〉 gently changes in the vicinity of the equilibrium stability as shown in Fig. S.16.
3.3. Equilibrium stability, ΔGe
The equilibrium value, ΔGe, of ΔG that satisfies 〈ΔΔGfixed〉=0 in fixed mutants depends directly on θ and indirectly on 4Neκ through fixation probability; see Eqs. (19) and (25). As shown in Fig. 5, ΔGe depends weakly on θ . On the other hand, ΔGe depends more strongly on and is almost negatively proportional to ![]() , as also shown in real proteins (Serohijos et al., 2013). If the dependence of the means, μs and μc in Eqs. (23) and (24), of ΔΔG in all mutants on ΔG could be neglected,
, as also shown in real proteins (Serohijos et al., 2013). If the dependence of the means, μs and μc in Eqs. (23) and (24), of ΔΔG in all mutants on ΔG could be neglected, ![]() could be regarded as a single parameter, and so
could be regarded as a single parameter, and so ![]() would be constant, irrespective of 4Neκ. Thus, the dependence of
would be constant, irrespective of 4Neκ. Thus, the dependence of ![]() on
on ![]() shown in Fig. 5 is caused solely by the linear dependence of the means μs and μc of ΔΔG on ΔG (Serohijos et al., 2012). It is interesting to know that as
shown in Fig. 5 is caused solely by the linear dependence of the means μs and μc of ΔΔG on ΔG (Serohijos et al., 2012). It is interesting to know that as ![]() varies from 0 to 20,ΔGe changes from
varies from 0 to 20,ΔGe changes from ![]() , the range of which is consistent with experimental values of protein folding free energies shown in Fig. 1.
, the range of which is consistent with experimental values of protein folding free energies shown in Fig. 1.

- Fig. 5.
Dependence of equilibrium stability, ΔGe, on parameters, 4Neκ and θ. ΔGe is the equilibrium value of folding free energy,ΔG, in protein evolution. The value of
 is the upper bound of
is the upper bound of  , and would be constant if the mean of ΔΔG in all arising mutants did not depend on ΔG; see Eq. (19). The kcal/mol unit is used for ΔGe.
, and would be constant if the mean of ΔΔG in all arising mutants did not depend on ΔG; see Eq. (19). The kcal/mol unit is used for ΔGe.
3.4. Ka/Ks at equilibrium, ΔG=ΔGe
Equations (23) and (24) indicate that the distribution of ΔΔG shifts toward the positive direction as ΔG becomes more negative. Hence, increasing 4Neκ that makes ΔGe more negative results in positive shifts of the distribution of ΔΔG, which increase destabilizing mutations. In addition, as indicated by Eq. (19), the upper bound of ![]() , scales the effect of ΔΔG on protein fitness. The larger
, scales the effect of ΔΔG on protein fitness. The larger ![]() is, the larger the effect of ΔΔG on selective advantage becomes. Thus, the increase of 4Neκexp(βΔGe) caused by the increase of κ and/or Ne increases both destabilizing mutations and their fitness costs, and results in slow evolutionary rates for proteins with large κ and/or Ne.
In other words, highly expressed and indispensable genes, and genes
with a large effective population size must evolve slowly. On the other
hand, the decrease of θ, that is, the increase of highly constrained residues directly shifts the average of ΔΔG in all arising mutants toward the positive direction, and causes slow evolutionary rates.
is, the larger the effect of ΔΔG on selective advantage becomes. Thus, the increase of 4Neκexp(βΔGe) caused by the increase of κ and/or Ne increases both destabilizing mutations and their fitness costs, and results in slow evolutionary rates for proteins with large κ and/or Ne.
In other words, highly expressed and indispensable genes, and genes
with a large effective population size must evolve slowly. On the other
hand, the decrease of θ, that is, the increase of highly constrained residues directly shifts the average of ΔΔG in all arising mutants toward the positive direction, and causes slow evolutionary rates.
The average of Ka/Ks
over all mutants, which can be observed as the ratio of average
nonsynonymous substitution rate per nonsynonymous site to average
synonymous substitution rate per synonymous site, and also that over
fixed mutants only are shown in Fig. 6. At any value of θ,〈Ka/Ks〉 decreases as ![]() increases, explaining the observed relationship that highly expressed and indispensable genes evolve slowly (Drummond et al., 2005, Drummond and Wilke, 2008 and Serohijos et al., 2012). Likewise, at any value of
increases, explaining the observed relationship that highly expressed and indispensable genes evolve slowly (Drummond et al., 2005, Drummond and Wilke, 2008 and Serohijos et al., 2012). Likewise, at any value of ![]() , 〈Ka/Ks〉 increases as θ
increases. In other words, the more structurally constrained a protein
is, the more slowly it evolves. The effect of protein
abundance/indispensability on evolutionary rate is more remarkable for
less constrained proteins and the effect of structural constraint is
more remarkable for less abundant, less essential proteins.
, 〈Ka/Ks〉 increases as θ
increases. In other words, the more structurally constrained a protein
is, the more slowly it evolves. The effect of protein
abundance/indispensability on evolutionary rate is more remarkable for
less constrained proteins and the effect of structural constraint is
more remarkable for less abundant, less essential proteins.
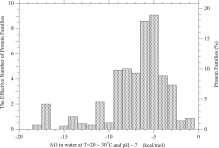
The average of Ka/Ks over all mutants, 〈Ka/Ks〉, is less than 1.0 on the whole domain shown in the figure, indicating that the average of Ka/Ks over a long time interval and over many sites should not show any positive selection. Even the average of Ka/Ks over fixed mutants is less than 1.0, and falls into a narrow range of 0.97–0.85, which is much narrower than a range of 0.96–0.15 for that over all mutants; the average of Ka/Ks over fixed mutants is equal to 〈(Ka/Ks)2〉/〈Ka/Ks〉, and as a matter of course must be equal to or larger than the averages of Ka/Ks over all mutants. However, the average of Ka/Ks over a short time interval and over a small number of sites may exhibit values larger than one. In Fig. 7, the PDFs of Ka/Ks for all mutants and also for fixed mutants only are shown; p(Ka/Ks)=p(4Nes)d(4Nes)/d(Ka/Ks). A significant fraction of fixed mutants fix with Ka/Ks>1.
Arbitrarily, the value of Ka/Ks is categorized into four classes; negative, slightly negative, nearly neutral, and positive selection categories whose Ka/Ks are within the range of Ka/Ks≤0.5,0.5<Ka/Ks≤0.95,0.95<Ka/Ks≤1.05, and 1.05<Ka/Ks,
respectively. Then, the probabilities of each selection category in all
mutants and in fixed mutants are calculated and shown in Fig. S.10 and Fig. 8, respectively. At the largest abundance (![]() ) most arising mutations are negative mutations whose Ka/Ks
are less than 0.5. This is reasonable, because at this condition the
wild-type protein is very stable with low equilibrium values ΔGe as shown in Fig. 5,
and therefore most mutations destabilize the wild-type and tend to be
removed from population. Most fixed mutants are positive mutants or
slightly negative mutants fixed by random drift. Nearly neutral mutants
are less than 3% of all mutants, and less than 15% of fixed mutants.
) most arising mutations are negative mutations whose Ka/Ks
are less than 0.5. This is reasonable, because at this condition the
wild-type protein is very stable with low equilibrium values ΔGe as shown in Fig. 5,
and therefore most mutations destabilize the wild-type and tend to be
removed from population. Most fixed mutants are positive mutants or
slightly negative mutants fixed by random drift. Nearly neutral mutants
are less than 3% of all mutants, and less than 15% of fixed mutants.

- Fig. 8.
Probability of each selection category in fixed mutants at equilibrium of protein stability, ΔG=ΔGe. Arbitrarily, the value of Ka/Ks is categorized into four classes; negative, slightly negative, nearly neutral, and positive selection categories in which Ka/Ks is within the ranges of Ka/Ks≤0.5,0.5<Ka/Ks≤0.95,0.95<Ka/Ks≤1.05, and 1.05<Ka/Ks, respectively.
On the other hand, at the other extreme of ![]() , there are no mutations of the positive selection category, this is because the upper bound of Ka/Ks, which corresponds to the upper bound (
, there are no mutations of the positive selection category, this is because the upper bound of Ka/Ks, which corresponds to the upper bound (![]() ) of 4Nes, at the equilibrium stability ΔGe becomes less than 1.05 that is the lower bound for the positive selection category; see Eq. (19). The significant amount of mutations become nearly neutral. As θ
changes from 1 to 0, that is, structural constraints increase, the
proportion of nearly neutral mutations changes from 0.75(0.56) to
0.31(0.22), and instead negative mutations increase and most of them are
removed from population. Thus, the selection mechanism for fixing
stabilizing mutants in little expressed, non-essential genes (
) of 4Nes, at the equilibrium stability ΔGe becomes less than 1.05 that is the lower bound for the positive selection category; see Eq. (19). The significant amount of mutations become nearly neutral. As θ
changes from 1 to 0, that is, structural constraints increase, the
proportion of nearly neutral mutations changes from 0.75(0.56) to
0.31(0.22), and instead negative mutations increase and most of them are
removed from population. Thus, the selection mechanism for fixing
stabilizing mutants in little expressed, non-essential genes (![]() ) is not positive selection but nearly neutral selection, that is, random drift.
) is not positive selection but nearly neutral selection, that is, random drift.
The probability of each selection category in fixed mutants depends strongly on 4Neκ, but much less on θ. Current common understanding is that amino acid substitutions in protein evolution are either neutral (Kimura, 1968) or lethal, at most slightly deleterious (Ohta, 1973)
or lethal, unless functional selection operates and functional changes
occur. On the contrary, nearly neutral fixations are predominant only in
proteins with ![]() or ΔGe>−2.5 kcal/mol,
and positive selection is significant in the other proteins. On the
other hand, slightly negative selection is always significant. An
interesting result is that the effects of structural constraint on Ka/Ks are the most remarkable in proteins with
or ΔGe>−2.5 kcal/mol,
and positive selection is significant in the other proteins. On the
other hand, slightly negative selection is always significant. An
interesting result is that the effects of structural constraint on Ka/Ks are the most remarkable in proteins with ![]() or instead ΔGe>−2.5 kcal/mol in which nearly neutral fixations are predominant.
or instead ΔGe>−2.5 kcal/mol in which nearly neutral fixations are predominant.
3.5. Ka/Ks in the vicinity of equilibrium
In Fig. 4, the 〈ΔΔG〉fixed± standard deviation of ΔΔG of fixed mutants are also drawn. The standard deviation of ΔΔG of fixed mutants is equal to 0.84 kcal/mol at the equilibrium, ΔGe, indicating that protein stability ΔG fluctuates more or less within ΔGe±0.84 kcal/mol instantaneously. Such a deviation from the equilibrium must be canceled by compensatory substitutions that consecutively occur, otherwise the protein stability would far depart from its equilibrium point.
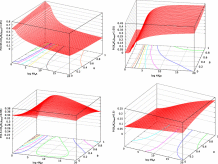
In Fig. 9 and Fig. 10 and Figs. S.12 and S.14, the probabilities of each selection category in fixed mutants and in all arising mutants are shown as a function of ΔG and 4Neκ or θ, respectively. The range of ΔG around ΔGe shown by a blue line on the surface grid is within two times of the standard deviation of ΔΔG over fixed mutants at ΔGe.

- Fig. 9.
Dependence of the probability of each selection category in fixed mutants on 4Neκ and ΔG. A blue line on the surface grid shows ΔG=ΔGe, which is the equilibrium value of ΔG in protein evolution. The range of ΔG shown in the figures is
 , where
, where  is the standard deviation of ΔΔG over fixed mutants at ΔG=ΔGe. Arbitrarily, the value of Ka/Ks is categorized into four classes; negative, slightly negative, nearly neutral, and positive selection categories in which Ka/Ks is within the ranges of Ka/Ks≤0.5,0.5<Ka/Ks≤0.95,0.95<Ka/Ks≤1.05, and 1.05<Ka/Ks, respectively. θ=0.53 is employed. The kcal/mol unit is used for ΔG.
(For interpretation of the references to color in this figure caption,
the reader is referred to the web version of this paper.)
is the standard deviation of ΔΔG over fixed mutants at ΔG=ΔGe. Arbitrarily, the value of Ka/Ks is categorized into four classes; negative, slightly negative, nearly neutral, and positive selection categories in which Ka/Ks is within the ranges of Ka/Ks≤0.5,0.5<Ka/Ks≤0.95,0.95<Ka/Ks≤1.05, and 1.05<Ka/Ks, respectively. θ=0.53 is employed. The kcal/mol unit is used for ΔG.
(For interpretation of the references to color in this figure caption,
the reader is referred to the web version of this paper.)

- Fig. 10.
Dependence of the probability of each selection category in fixed mutants on θ and ΔG. A blue line on the surface grid shows ΔG=ΔGe, which is the equilibrium value of ΔG in protein evolution. The range of ΔG shown in the figures is
 , where
, where  is the standard deviation of ΔΔG over fixed mutants at ΔG=ΔGe. Arbitrarily, the value of Ka/Ks is categorized into four classes; negative, slightly negative, nearly neutral, and positive selection categories in which Ka/Ks is within the ranges of Ka/Ks≤0.5,0.5<Ka/Ks≤0.95,0.95<Ka/Ks≤1.05, and 1.05<Ka/Ks, respectively.
is the standard deviation of ΔΔG over fixed mutants at ΔG=ΔGe. Arbitrarily, the value of Ka/Ks is categorized into four classes; negative, slightly negative, nearly neutral, and positive selection categories in which Ka/Ks is within the ranges of Ka/Ks≤0.5,0.5<Ka/Ks≤0.95,0.95<Ka/Ks≤1.05, and 1.05<Ka/Ks, respectively.  is employed. The kcal/mol unit is used for ΔG.
(For interpretation of the references to color in this figure caption,
the reader is referred to the web version of this paper.)
is employed. The kcal/mol unit is used for ΔG.
(For interpretation of the references to color in this figure caption,
the reader is referred to the web version of this paper.)
As indicated by Eqs. (23) and (24), it is shown in Figs. S.12 and S14 that stabilizing mutations increase due to negative shifts of ΔΔG as the wild type becomes less stable than the equilibrium, ΔG>ΔGe, and that destabilizing mutations increase due to positive shifts of ΔΔG as ΔG<ΔGe. In addition, as indicated by Eq. (19), it is shown in Fig. 9 and Fig. 10 that positive selection on stabilizing mutants is more amplified as ΔG>ΔGe, and that more destabilizing mutations become nearly neutral due to the less-amplified effect of stability change on selective advantage as ΔG<ΔGe. This is a mechanism of maintaining protein stability at equilibrium.
3.6. Lower bound of Ka/Ks for adaptive substitutions on protein function
The observed value of Ka/Ks>1 is often used to indicate functional selection. The averages of Ka/Ks over all mutants and even over fixed mutants are less than 1 as shown in Fig. 6. Therefore, the average of Ka/Ks over long time or many sites does not indicate positive selection. However, the probability of Ka/Ks>1 is not negligible as shown in Fig. 7 and Fig. 8. Then, a question is how large Ka/Ks due to selection on protein stability can be.
The distribution of Ka/Ks significantly changes with ΔG, as shown in Fig. S.6 and Fig. 11. It may be appropriate to see the average of Ka/Ks,〈Ka/Ks〉fixed, in mutants fixed at ΔG>ΔGe, because the upper bound of Ka/Ks becomes larger for ΔG>ΔGe than at the equilibrium, and also positive mutants must fix to improve the protein stability of the wild type. Fig. 11 shows that 〈Ka/Ks〉fixed can be very large for proteins with low equilibrium stabilities (large 4Neκ and small θ), although 〈Ka/Ks〉fixed ~ 1in ΔG < ΔGe in which nearly neutral and slightly negative selections are predominant 1.7(1.2) at ![]() and 6.1(5.6) at
and 6.1(5.6) at ![]() for
for ![]() , where
, where ![]() means the standard deviation of ΔΔG in fixed mutants at ΔGe. The 85% of fixed mutants have ΔΔG
within the standard deviation. Therefore, a lower bound for adaptive
substitutions may be taken to be about 1.7, which is almost equal to the
upper bound of Ka/Ks at the equilibrium for
means the standard deviation of ΔΔG in fixed mutants at ΔGe. The 85% of fixed mutants have ΔΔG
within the standard deviation. Therefore, a lower bound for adaptive
substitutions may be taken to be about 1.7, which is almost equal to the
upper bound of Ka/Ks at the equilibrium for ![]() and θ=1;
see Fig. S.17. However, as shown in Fig. S.17, the more genes are
expressed and/or the stronger structural constraints are, the larger the
upper bound of Ka/Ks at the equilibrium is. Judging of adaptive changes may need not only Ka/Ks>1 but also other supporting evidences; such that substitutions are localized at specific sites.
and θ=1;
see Fig. S.17. However, as shown in Fig. S.17, the more genes are
expressed and/or the stronger structural constraints are, the larger the
upper bound of Ka/Ks at the equilibrium is. Judging of adaptive changes may need not only Ka/Ks>1 but also other supporting evidences; such that substitutions are localized at specific sites.

- Fig. 11.
Dependence of the average of Ka/Ks over all mutants or over fixed mutants only on protein stability, ΔG, of the wild type. A blue line on the surface grid shows ΔG=ΔGe, which is the equilibrium value of ΔG in protein evolution. The range of ΔG shown in the figures is
 , where
, where  is the standard deviation of ΔΔG over fixed mutants at ΔG=ΔGe. Unless specified,
is the standard deviation of ΔΔG over fixed mutants at ΔG=ΔGe. Unless specified,  and θ=0.53 are employed. The kcal/mol unit is used for ΔG.
(For interpretation of the references to color in this figure caption,
the reader is referred to the web version of this paper.)
and θ=0.53 are employed. The kcal/mol unit is used for ΔG.
(For interpretation of the references to color in this figure caption,
the reader is referred to the web version of this paper.)
3.7. Dependences of protein stability (βΔGe) and evolutionary rate (〈Ka/Ks〉) on growth temperature
It is natural that the folding free energies, ΔGe,
of proteins in organisms growing at higher temperatures must be lower
than those at the normal temperature, in order to attain the same
stabilities and fitnesses as in the normal temperature. Equations (2) and (15) indicate that the same stability and fitness will be attained if βΔGe is constant. It means that it is sufficient for ΔGe at the ![]() to decrease 373/298=1.25 times of that at the normal temperature
to decrease 373/298=1.25 times of that at the normal temperature ![]() .
Is this a figure expected for folding free energies of thermophilic
proteins at high growth temperature? It is not enough data of ΔG at high temperature in the ProTherm (Kumar et al., 2006) to answer this question;
.
Is this a figure expected for folding free energies of thermophilic
proteins at high growth temperature? It is not enough data of ΔG at high temperature in the ProTherm (Kumar et al., 2006) to answer this question; ![]() kcal/mol for oxidized and 4.3 for reduced CuA domain of cytochrome oxidase from Thermus thermophilus (Wittung-Stafshede et al., 1998) and
kcal/mol for oxidized and 4.3 for reduced CuA domain of cytochrome oxidase from Thermus thermophilus (Wittung-Stafshede et al., 1998) and ![]() kcal/mol for pyrrolidone carboxyl peptidase from Pyrococcus (Ogasahara et al., 1998). The present model indicates that βΔGe slightly increases as growth temperature increases.
kcal/mol for pyrrolidone carboxyl peptidase from Pyrococcus (Ogasahara et al., 1998). The present model indicates that βΔGe slightly increases as growth temperature increases.
In Fig. 12 and Fig. S.18, ![]() is shown as a function of absolute temperature T and
is shown as a function of absolute temperature T and ![]() or θ, assuming that the distribution of ΔΔG and its dependency on ΔG do not depend on T, that is, Eqs. (22), (23) and (24). At fixed values of
or θ, assuming that the distribution of ΔΔG and its dependency on ΔG do not depend on T, that is, Eqs. (22), (23) and (24). At fixed values of ![]() and
and ![]() increases as T increases, meaning that protein stability, −βΔG, decreases as growth temperature increases. This tendency is slightly larger at smaller values of
increases as T increases, meaning that protein stability, −βΔG, decreases as growth temperature increases. This tendency is slightly larger at smaller values of ![]() , that is, for less abundant proteins.
, that is, for less abundant proteins.

- Fig. 12.
Dependence of equilibrium stability, ΔGe, on parameters, 4Neκ and T. ΔGe is the equilibrium value of folding free energy, ΔG, in protein evolution. T is absolute temperature; β=1/kT, where k is the Boltzmann constant. Equations (22), (23) and (24) are assumed for the distribution of ΔΔG and its dependency on ΔG; they are assumed to be independent of T. θ=0.53 is employed. The value of
 is the upper bound of
is the upper bound of  , and would not depend on
, and would not depend on  if the mean of ΔΔG in all arising mutants did not depend on ΔG; see Eq. (19). The kcal/mol unit is used for ΔGe.
if the mean of ΔΔG in all arising mutants did not depend on ΔG; see Eq. (19). The kcal/mol unit is used for ΔGe.
The effects of growth temperature on Ka/Ks are shown in Fig. S.19. The present model predicts that 〈Ka/Ks〉 decreases as growth temperature increases unless any other parameter does not change.
4. Discussion
Recently, fitness costs due to misfolded proteins have been widely noticed, particularly neurological disorder linked to misfolded protein toxicity (Bucciantini et al., 2002). Fitness costs that originate in functional loss (Geiler-Samerotte et al., 2011) and in diversion of protein synthesis and aggregation of proteins have been evaluated (Drummond and Wilke, 2008) to be related to the proportion of misfolded proteins. Also, previous studies indicate that factors that relate protein stability to protein fitness are protein abundance, protein indispensability, and structural constraints of protein. Current knowledge of protein folding can provide an exact formulation for the proportion of misfolded proteins as a function of folding free energy, and reasonable predictions (Schymkowitz et al., 2005, Yin et al., 2007 and Tokuriki et al., 2007) of stability changes due to single amino acid substitutions in protein native structures. Thus, on the basis of knowledge of protein biophysics it became possible to study the effects of amino acid substitutions on protein stability and then the evolution of protein (Drummond and Wilke, 2008, Serohijos et al., 2012, Serohijos and Shakhnovich, 2014, Echave et al., 2015 and Faure and Koonin, 2015).
Here, the effects of protein abundance and indispensability (κ) and of structural constraint (θ) on protein evolutionary rate (Ka/Ks) have been examined in detail. Both the effects are represented with different functional forms. Structural constraints affect the distribution of stability change ΔΔG due to mutations. On the other hand, protein abundance/indispensability affects the effectiveness of stability change on protein fitness as well as the distribution of ΔΔG.
The
common understanding of protein evolution has been that amino acid
substitutions found in homologous proteins are selectively neutral (Kimura, 1968, Kimura, 1969, Kimura and Ohta, 1971 and Kimura and Ohta, 1974) or slightly deleterious (Ohta, 1973 and Ohta, 1992),
and random drift is a primary force to fix amino acid substitutions in
population. However, there is a selection maintaining protein stability
at equilibrium (Drummond and Wilke, 2008, Serohijos et al., 2012 and Serohijos and Shakhnovich, 2014). From the present analysis of the PDF of Ka/Ks, it has become clear how the equilibrium of stability is maintained; see Fig. 9 and Fig. 10. In less-stable proteins of ΔG>ΔGe, more stabilizing mutations fix due to positive selection, because negative shifts of ΔΔG increase stabilizing mutants and also more amplify the effect of stability change on selective advantage; see Eqs. (23), (24) and (19). In more-stable proteins of ΔG<ΔGe, more destabilizing mutants are fixed by random drift, because positive shifts of ΔΔG
increase destabilizing mutants and also make more destabilizing mutants
become nearly neutral with the less-amplified effect of stability
change on selective advantage. It has been revealed that contrary to the
neutral theory nearly neutral selection is predominant only in
low-abundant, non-essential proteins with ![]() or with low equilibrium stability
or with low equilibrium stability ![]() ; see Fig. 8.
; see Fig. 8.
The average 〈Ka/Ks〉 and even 〈Ka/Ks〉fixed at equilibrium stability ΔG=ΔGe are less than one over the whole parameter range; see Fig. 6. Hence, as far as selection is on protein stability, the average of Ka/Ks over a long time interval and over many sites will be expected to be less than one, if all synonymous mutations are neutral (Spielman and Wilke, 2015). However, because the probability of Ka/Ks>1 is significant, branches with Ka/Ks>1 in phylogenetic trees may be observed, as observed in a population dynamics simulation (Serohijos and Shakhnovich, 2014), even though synonymous mutations are neutral and no adaptive selection operates on protein function. According to the present estimate, a lower bound of Ka/Ks to indicate adaptive substitutions must be at least as large as 1.7.
Protein equilibrium stability (ΔGe) has been clearly described here as a function of 4Neκ and θ. The more expressed a gene is (the larger 4Neκ is), the stabler the wild-type protein at equilibrium is (the more negative ΔGe becomes); see Fig. 5. The decrease of ΔGe shifts the distribution of ΔΔG toward the positive direction, generating more highly destabilizing mutants; see Eqs. (23) and (24). In addition, as 4Neκ increases, the net effect, ![]() , increases and more amplifies the effects of stability changes (ΔΔG) on selective advantage (s); see Fig. 5 and Eq. (19). As a result, highly expressed and indispensable genes, and genes with a large effective population size evolve slowly; see Fig. 6. However, if the distribution of ΔΔG did not depend on ΔG,
, increases and more amplifies the effects of stability changes (ΔΔG) on selective advantage (s); see Fig. 5 and Eq. (19). As a result, highly expressed and indispensable genes, and genes with a large effective population size evolve slowly; see Fig. 6. However, if the distribution of ΔΔG did not depend on ΔG, ![]() would be constant, and Ka/Ks would not depend on 4Neκ, that is, protein abundance/indispensability and effective population size.
would be constant, and Ka/Ks would not depend on 4Neκ, that is, protein abundance/indispensability and effective population size.
On the other hand, structural constraints on protein affect protein evolutionary rate by changing the distribution of ΔΔG due to amino acid substitutions. As shown in Fig. 6, at any value of ![]() , 〈Ka/Ks〉 decreases as θ decreases. In other word, the more a protein is structurally constrained, the more slowly it evolves, as claimed by Zuckerkandl (1976). Fig. 6
shows that the effect of protein abundance/indispensability on
evolutionary rate is more remarkable for less constrained proteins, and
the effect of structural constraint is more remarkable for less
abundant, less essential proteins.
, 〈Ka/Ks〉 decreases as θ decreases. In other word, the more a protein is structurally constrained, the more slowly it evolves, as claimed by Zuckerkandl (1976). Fig. 6
shows that the effect of protein abundance/indispensability on
evolutionary rate is more remarkable for less constrained proteins, and
the effect of structural constraint is more remarkable for less
abundant, less essential proteins.
In the result, the average of Ka/Ks over all arising mutants decreases roughly by 0.4–0.8 as ![]() increases from 0 to 20; see Fig. 6. On the other hand, it decreases by 0.1–0.4 as the proportion of the residues of the surface type, θ,
decreases from 1 to 0. For monomeric, globular proteins, the proportion
of protein surface may range from 0.7 to 0.45. Thus, in typical
globular proteins, protein abundance/indispensability may cause larger
differences of evolutionary rate between proteins than structural
constraint. However, proteins that interact with other molecules on
protein surface effectively reduce residues of the protein-surface type (Franzosa and Xia, 2009). Both protein abundance/indispensability and structural constraint must be taken into account for protein evolutionary rate.
increases from 0 to 20; see Fig. 6. On the other hand, it decreases by 0.1–0.4 as the proportion of the residues of the surface type, θ,
decreases from 1 to 0. For monomeric, globular proteins, the proportion
of protein surface may range from 0.7 to 0.45. Thus, in typical
globular proteins, protein abundance/indispensability may cause larger
differences of evolutionary rate between proteins than structural
constraint. However, proteins that interact with other molecules on
protein surface effectively reduce residues of the protein-surface type (Franzosa and Xia, 2009). Both protein abundance/indispensability and structural constraint must be taken into account for protein evolutionary rate.
Protein abundance and indispensability both affect evolutionary rate similarly through protein fitness. It was shown in real proteins that protein abundance correlates with evolutionary rate (Pál et al., 2001). The present model of protein fitness Eq. (19) also indicates that protein indispensability must correlate with evolutionary rate (Hirsh and Fraser, 2001, 2003), but a correlation between them may be hidden by the variation of protein abundance and detected only in low-abundant proteins (Pál et al., 2003); see Eq. (21). In addition, effective population size must affect ΔGe and 〈Ka/Ks〉 together with κ as 4Neκ.
In the present model, protein equilibrium stability (ΔGe) and evolutionary rate (〈Ka/Ks〉) are predictable from θ and 4Neκ. The proportion of the surface type of residues may be estimated as those whose surface accessibility values (ASA) are less than 0.25 (Tokuriki et al., 2007), but experimental measurements of protein abundance, indispensability, and effective population size to determine 4Neκ may be relatively hard. Instead the experimental value of protein stability may be employed as equilibrium stability to predict evolutionary rate and others, although it is not an independent variable. Fig. 13 shows evolutionary rate as a function of ΔGe and θ. Needless to say, mutational effects on ΔΔG, such as θ and the distribution of ΔΔG, must be well estimated for various categories of proteins (Faure and Koonin, 2015) to obtain successful predictions. Also, accurate estimations of ΔG for various proteins are needed to examine the present predictions. It is interesting to examine if protein stability (−βΔG) and the average of Ka/Ks decrease as growth temperature increases.
5. Conclusions
- •
The range,
 , of equilibrium values, ΔGe,
of protein stability calculated with the present fitness model is
consistent with the distribution of experimental values shown in Fig. 1.
, of equilibrium values, ΔGe,
of protein stability calculated with the present fitness model is
consistent with the distribution of experimental values shown in Fig. 1.- •
Contrary to the neutral theory, nearly neutral selection is predominant only in low-abundant, non-essential proteins of
 or ΔGe>−2.5 kcal/mol.
In the other proteins, positive selection on stabilizing mutations is
significant to maintain protein stability at equilibrium as well as
random drift on slightly negative mutations. However, 〈Ka/Ks〉 and even 〈Ka/Ks〉fixed at ΔG=ΔGe are less than 1.
or ΔGe>−2.5 kcal/mol.
In the other proteins, positive selection on stabilizing mutations is
significant to maintain protein stability at equilibrium as well as
random drift on slightly negative mutations. However, 〈Ka/Ks〉 and even 〈Ka/Ks〉fixed at ΔG=ΔGe are less than 1.- •
Protein abundance/indispensability (κ) and effective population size (Ne) more affect evolutionary rate for less constrained proteins, and structural constraint (θ) for less abundant, less essential proteins.
- •
Protein indispensability must negatively correlate with evolutionary rate like protein abundance, but the correlation between them may be hidden by the variation of protein abundance and detected only in low-abundant proteins.
- •
Evolutionary rates of proteins may be predicted from equilibrium stability (ΔGe) and structural constraints (PDF of ΔΔG) of the protein.
- •
The present model indicates that protein stability (−βΔGe) and 〈Ka/Ks〉 decrease as growth temperature increases.
Appendix A. Supplementary data
References
- Bucciantini et al., 2002
Inherent toxicity of aggregates implies a common mechanism for protein misfolding diseases
Nature, 416 (2002), pp. 507–511

- Crow and Kimura, 1970
An Introduction to Population Genetics Theory
Harper & Row publishers, New York (1970)

- Dasmeh et al., 2014
The influence of selection for protein stability on dN/dS estimations
Genome Biol. Evol., 6 (2014), pp. 2956–2967

- Drummond and Wilke, 2008
Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution
Cell, 134 (2) (2008), pp. 341–352 http://dx.doi.org/10.1016/j.cell.2008.05.042

- Duret and Mouchiro, 2000
Determinants of substitution rates in mammalian genes: expression pattern affects selection intensity but not mutation rate
Mol. Biol. Evol., 17 (2000), pp. 68–85

- Echave et al., 2015
Relationship between protein thermodynamic constraints and variation of evolutionary rates among sites
Phys. Biol., 12 (2) (2015), p. 025002 〈http://stacks.iop.org/1478-3975/12/i=2/a=025002〉

- Faure and Koonin, 2015
Universal distribution of mutational effects on protein stability, uncoupling of protein robustness from sequence evolution and distinct evolutionary modes of prokaryotic and eukaryotic proteins
Phys. Biol., 12 (3) (2015), p. 035001 〈http://stacks.iop.org/1478-3975/12/i=3/a=035001〉

- Franzosa and Xia, 2009
Structural determinants of protein evolution are context-sensitive at the residue level
Mol. Biol. Evol., 26 (2009), pp. 2387–2395

- Fraser et al., 2002
Evolutionary rate in the protein interaction network
Science, 296 (2002), pp. 750–752

- Ghaemmaghami et al., 2003
Global analysis of protein expression in yeast
Nature, 425 (2003), pp. 737–741

- Go and Miyazawa, 1980
Relationship between mutability, polarity and exteriority of amino acid residues in protein evolution
Int. J. Pept. Protein Res., 15 (1980), pp. 211–224

- Hirsh and Fraser, 2001
Protein dispensability and rate of evolution
Nature, 411 (2001), pp. 1047–1049

- Hirsh and Fraser, 2003
Genomic function (communication arising): rate of evolution and gene dispensability
Nature, 421 (2003), pp. 497–498

- Jordan et al., 2002
Essential genes are more evolutionarily conserved than are nonessential genes in bacteria
Genome Res., 12 (2002), pp. 962–968

- Kimura, 1968
Evolutionary rate at the molecular level
Nature, 217 (1968), pp. 624–626

- Kimura and Ohta, 1971
Protein polymorphism as a phase of molecular evolution
Nature, 229 (1971), pp. 467–469

- Kuma et al., 1995
Functional constraints against variations on molecules from the tissue level: slowly evolving brain-specific genes demonstrated by protein kinase and immunoglobulin supergene families
Mol. Biol. Evol., 12 (1995), pp. 123–130

- Kumar et al., 2006
ProTherm and ProNIT: thermodynamic databases for proteins and protein-nucleic acid interactions
Nucl. Acid Res., 34 (2006), pp. D204–D206

- Lynch and Conery, 2003
The origins of genome complexity
Science, 302 (2003), pp. 1401–1404

- Miyata and Yasunaga, 1980
Molecular evolution of mRNA: a method for estimating evolutionary rates of synonymous and amino acid substitutions from homologous nucleotide sequences and its applications
J. Mol. Evol., 16 (1980), pp. 23–36

- Miyazawa and Jernigan, 1982a
Equilibrium folding and unfolding pathways for a model protein
Biopolymers, 21 (1982), pp. 1333–1363

- Miyazawa and Jernigan, 1982b
Most probable intermediates in protein folding-unfolding with a non-interacting globule-coil model
Biochemistry, 21 (1982), pp. 5203–5213

- Ogasahara et al., 1998
The unusually slow unfolding rate causes the high stability of pyrrolidone carboxyl peptidase from a hyperthermophile, Pyrococcus furiosus: equilibrium and kinetic studies of guanidine hydrochloride-induced unfolding and refolding
Biochemistry, 37 (1998), pp. 17537–17544

- Ohta, 1973
Slightly deleterious mutant substitutions in evolution
Nature, 246 (1973), pp. 96–98

- Ohta, 1992
The nearly neutral theory of molecular evolution
Annu. Rev. Ecol. Syst., 23 (1992), pp. 263–286

- Pál et al., 2001
Highly expressed genes in yeast evolve slowly
Genetics, 158 (2001), pp. 927–931

- Pál et al., 2003
Genomic function (communication arising): rate of evolution and gene dispensability
Nature, 421 (2003), pp. 496–497

- Schymkowitz et al., 2005
The FoldX web server: an online force field
Nucl. Acid Res., 33 (2005), pp. W382–W388

- Serohijos et al., 2012
Protein biophysics explains why highly abundant proteins evolve slowly
Cell Rep., 2 (2) (2012), pp. 249–256 〈http://dx.doi.org/10.1016/j.celrep.2012.06.022〉

- Serohijos et al., 2013
Highly abundant proteins favor more stable 3D structures in yeast
Biophys. J., 104 (3) (2013), pp. L1–L3 http://dx.doi.org/10.1016/j.bpj.2012.11.3838

- Serohijos and Shakhnovich, 2014
Contribution of selection for protein folding stability in shaping the patterns of polymorphisms in coding regions
Mol. Biol. Evol., 31 (2014), pp. 165–176

- Spielman and Wilke, 2015
The relationship between dN/dS and scaled selection coefficients
Mol. Biol. Evol., 32 (2015), pp. 1097–1108

- Stoebel et al., 2008
The cost of expression of Escherichia coli lac operon proteins ss in the process, not in the product
Genetics, 178 (2008), pp. 1653–1660

- Tokuriki et al., 2007
The stability effects of protein mutations appear to be universally distributed
J. Mol. Biol., 369 (2007), pp. 1318–1332

- Wittung-Stafshede et al., 1998
Effect of redox state on the folding free energy of a thermostable electron-transfer metalloprotein: the CuA domain of cytochrome oxidase from thermus thermophilus
Biochemistry, 37 (1998), pp. 3172–3177

- Yin et al., 2007
Eris: an automated estimator of protein stability
Nat. Methods, 4 (2007), pp. 466–467

- Zhang and He, 2005
Significant impact of protein dispensability on the instantaneous rate of protein evolution
Mol. Biol. Evol., 22 (2005), pp. 1147–1155

- Zuckerkandl, 1976
Evolutionary processes and evolutionary noise at the molecular level
J. Mol. Evol., 7 (1976), pp. 167–183

Copyright © 2015 Elsevier Ltd. All rights reserved.